The curse of dimensionality

One would think that the more features one has to describe samples in a dataset the better one would be able to perform a classification task. Unfortunately with the increase of the number of features comes the difficulty of fitting a multi-dimensional model.

This is generally referred to as the curse of dimensionality and we will see a few surprising effects that explain why more features can make life difficult.

How many points are in the center of the cube?

We can ask the question "In the hypercube $-1\leq x_i\leq 1$, how many points are no further apart to the center than 1?"

This is equivalent to asking what is the ratio of the unit "ball" to the volume of the smallest "cube" enclosing it.

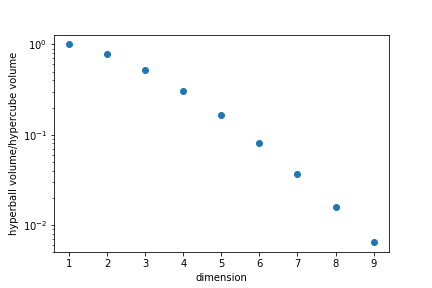
In high dimensions most points are in "corners" rather than in the "centre".

Average distance between two random points

Looking at the unit cube, we can calculate the average distance between any two points.

$$ d=\sqrt{\sum_i x_i^2} $$

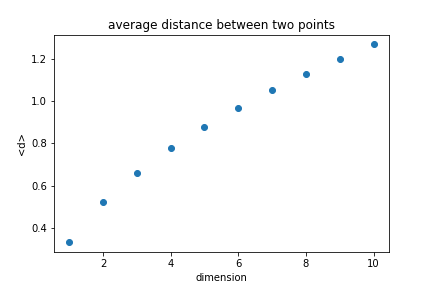
The average distance increases with the dimension.

We can also plot the distribution of distances:

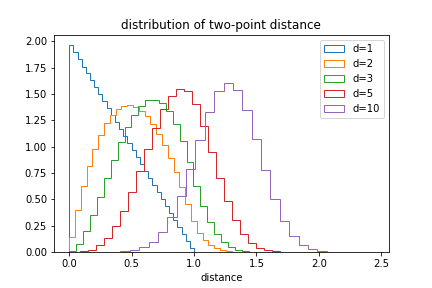
The likelihood of small distances drops as the dimension increases.

Proximity to edges

One interesting question to ask is how close to the edges points are. To quantify it we will calculate what is the thickness $t$ of the outer layer of the unit cube that contain half the points if the points are randomly distributed.

The volume inside is given by

$$ V_i = (1-2t)^d \qquad V_i=\frac12 \Rightarrow t = \frac{1-2^{-1/d}}{2}$$

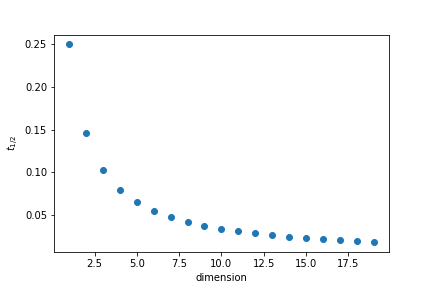
In 35 dimensions half of the points are in a outer layer 0.01 thin.