Variance Bias Trade-off

Let's suppose the relationship between $X$ and $Y$ is described by

$$ Y = \sum_i w_i^\star x^i + \epsilon$$

where $w_i^\star$ are the true parameters and $\epsilon$ is some noise.

We will try to model this with

$$ y = p(x) = \sum_i w_i x^i$$

where now the $w_i$ will be fitted to data.

We define

$$ \bar w_i = \langle w_i\rangle $$

as the expectation value of the parameter $w_i$ when fitted to multiple independent samples drawn from the true distribution.

We want to calculate the expected deviation of the fitted coefficients form the true coefficient:

$$ \langle (w_i-w_i^\star)^2\rangle$$

$$ \begin{eqnarray} \langle (w_i-w_i^\star)^2\rangle & = & \langle (w_i-\bar w_i +\bar w_i -w_i^\star)^2\rangle \\ &=& \langle (w_i-\bar w_i)^2\rangle + \langle (\bar w_i-w_i^\star)^2\rangle +2 \langle (w_i-\bar w_i)(\bar w_i -w_i^\star)\rangle \end{eqnarray}$$

The third term vanishes: $$ \langle (w_i-\bar w_i)(\bar w_i -w_i^\star)\rangle = \langle (w_i-\bar w_i)\rangle (\bar w_i -w_i^\star) =0 $$

So we have

$$ \langle (w_i-w_i^\star)^2\rangle = \langle (w_i-\bar w_i)^2\rangle + \langle (\bar w_i-w_i^\star)^2\rangle$$

The first term is the variance term and the second is the bias.

Example

To illustrate the variance-bias tradeoff we will be using different models to describe data with true relationship between the input $x$ and the outcome

$$Y(x) = 1+\frac15 x^2 + \epsilon \qquad \mbox{for}\qquad 0\leq x\leq 1\;, \quad 0 \; \mbox{otherwise}$$

Where $\epsilon$ is a gaussian noise. We will use the two models

$$ m_1(x) = a +bx$$

and

$$m_2(x)= a+bx +cx^2 +dx^3.$$

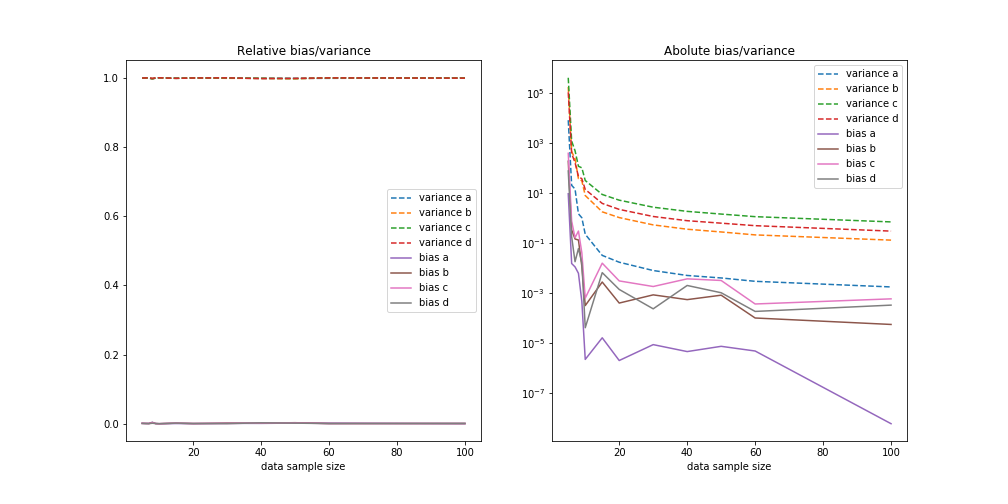
Using $m_1$, a model with too few parameters we get

For low dataset size we see the the variance dominates but as the number of training samples grows the bias dominates. Since the model is not capable of describing the truth the error is not diminishing even though the variance part of the error drops proportional to $1/\sqrt{N}$

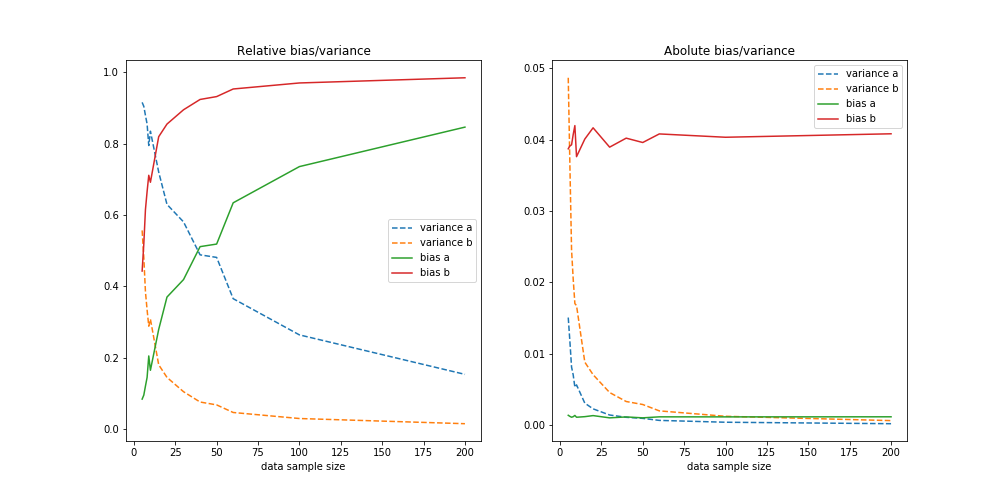
For the second model where we have enough freedom to exactly describe the truth we get: